Laplacian2Mesh: Laplacian-Based Mesh Understanding

Abstract

Geometric deep learning has sparked a rising interest in computer graphics to perform shape understanding tasks, such as shape classification and semantic segmentation. When the input is a polygonal surface, one has to suffer from the irregular mesh structure. Motivated by the geometric spectral theory, we introduce Laplacian2Mesh, a novel and flexible convolutional neural network (CNN) framework for coping with irregular triangle meshes (vertices may have any valence). By mapping the input mesh surface to the multi-dimensional Laplacian-Beltrami space, Laplacian2Mesh enables one to perform shape analysis tasks directly using the mature CNNs, without the need to deal with the irregular connectivity of the mesh structure. We further define a mesh pooling operation such that the receptive field of the network can be expanded while retaining the original vertex set as well as the connections between them. Besides, we introduce a channel-wise self-attention block to learn the individual importance of feature ingredients. Laplacian2Mesh not only decouples the geometry from the irregular connectivity of the mesh structure but also better captures the global features that are central to shape classification and segmentation. Extensive tests on various datasets demonstrate the effectiveness and efficiency of Laplacian2Mesh, particularly in terms of the capability of being vulnerable to noise to fulfill various learning tasks.

Introduction

In this paper, we propose Laplacian2Mesh, inheriting the spirit of those spectral approaches, to make it possible to conduct learning tasks in the spectral domain when the input is a polygonal mesh. Note that the main technique of spectral approaches is to encode the overall shape by a subset of the eigenvectors decomposed from the Laplacian matrix of the input mesh. Two reasons account for why we advocate using the new representation in deep learning. First, as the low-frequency signals, given by those eigenvectors with small eigenvalues, encode the overall shape, they are more semantically important than high-frequency signals for most understanding tasks. It is easy for one to separate low-frequency signals from high-frequency signals in spectral approaches by setting a simple parameter k. Second, the Laplacian-based spectral transform can decouple shape variations from the tedious triangulation, avoiding tangling with tedious and irregular triangulations. Even if the input mesh contains a limited number of defects (e.g., non-manifold), the representation still works.

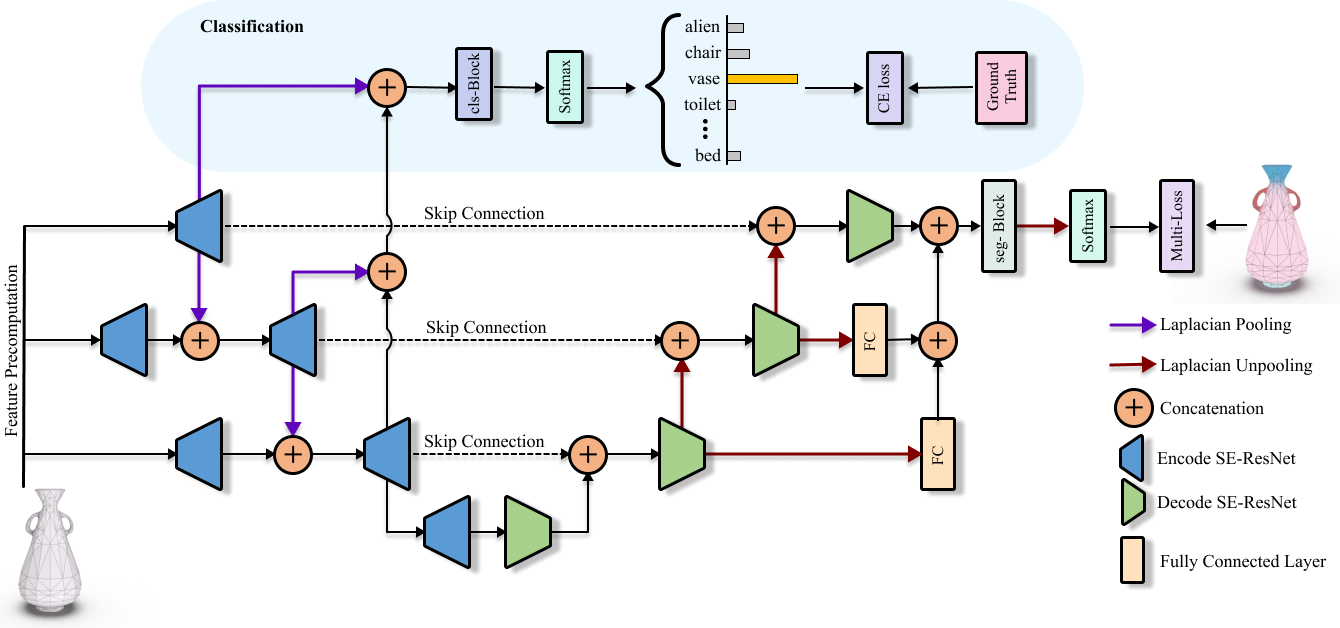
Pipeline of Laplacian2Mesh.

Our network pipeline for coping with the mesh classification and segmentation tasks. Given a 3D mesh as the input, we precompute the extrinsic and intrinsic geometric features and project them into the spectral domain w.r.t. three different resolutions. Inspired by the U-Net architecture, we propose to use the SE-ResNet blocks with small-sized convolution kernels to fuse the nearby-frequency features, and the Laplacian pooling/unpooling to fuse the spectral features of different resolutions. For the segmentation task, we re-scale (with the yellow block) and concatenate the features together to be processed by the segmentation block.

Pooling and Unpooling of Laplacian2Mesh.

The Laplacian pooling and unpooling operations transform the spectral-based features between different resolutions, where the pooling operation proceeds from a finer level to a coarser level while the unpooling operation does the opposite.

Results

Gallery of segmentation results for the COSEG dataset. From left to right, they are Tele-aliens, Chairs, and Vases.

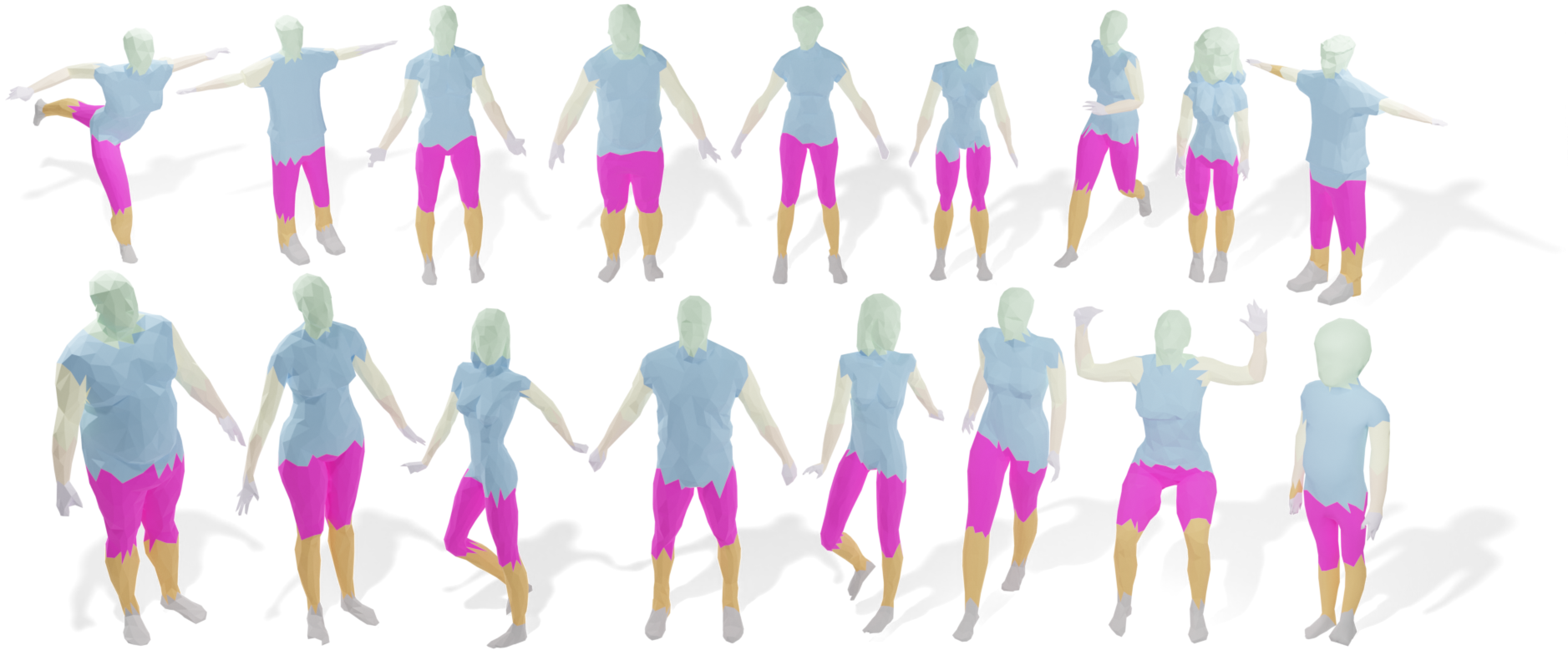
We test the dataset of Human Body, and visualize the segmentation result for every model.

Strengths

Laplacian2Mesh combines the geometric spectral theory with deep learning, which overcomes the challenges of dealing with the irregular connectivity of meshes, and is a promising direction to understand 3D shapes in a tessellation independent manner. Our network inherits some merits of spectral analysis approaches. First, it can encode the shape features in various levels (from local to global) and naturally has a noise-resistance ability. Second, it is independent of mesh resolution/tesselation and can handle non-watertight, non-manifold, and incomplete triangle-meshes.

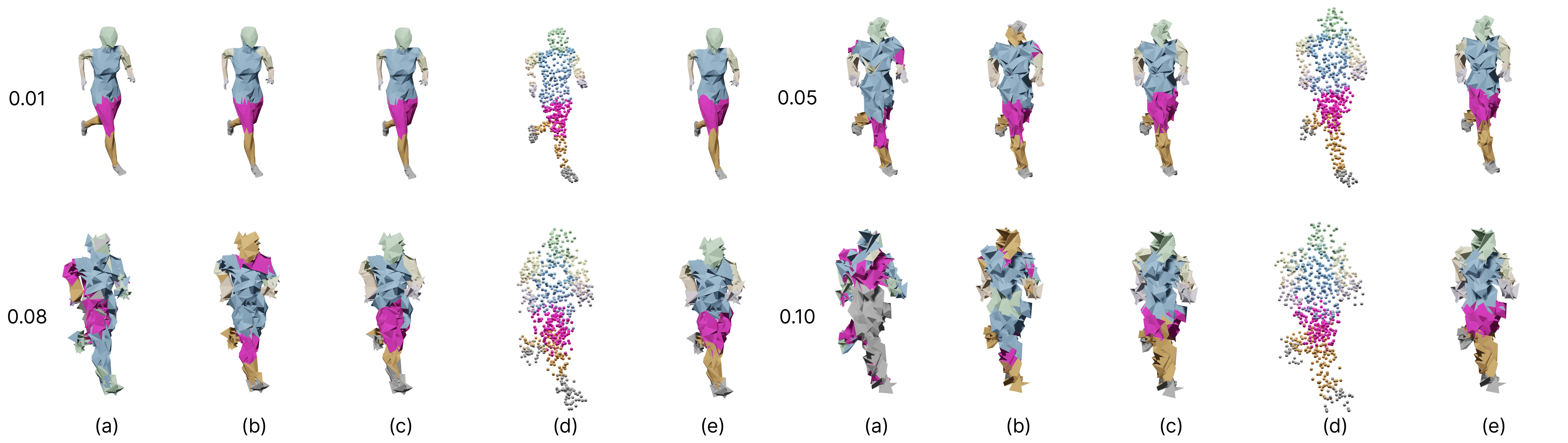
The qualitative results of testing the noise-resistance. As noise levels rise, segmentation outputs of DiffusionNet diverge significantly from the ground-truth, while ours is more in line with it. Numbers are levels of Gaussian noise added.
(a) DiffusionNet-hks; (b) DiffusionNet-xyz; (c) Laplacian2Mesh; (d) Laplacian2Mesh (point cloud); (e) Ground-Truth.

Our Laplacian2Mesh is able to perform segmentation on the nonwatertight and non-manifold data. (a) and (b) are non-watertight vases and chairs, respectively; (c) has a non-manifold vertex, and (d) has a non-manifold edge.

The results on incomplete models. The red dashed boxes on the mesh indicate the deleted parts. The green dashed boxes highlight the inaccurate segmentation boundaries.